Question

Which graph represents the function f(x)=1/x+3-2

Answer 1

files are attached below

Answer 2

The graph as shown below.

Explanation:

Given : The function
`f(x)=(1)/(x-3)-2`

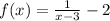
We have to plot the graph for the given function
`f(x)=(1)/(x-3)-2`

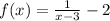
Consider the given function
`f(x)=(1)/(x-3)-2`

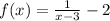
Domain of function
`f(x)=(1)/(x-3)-2`

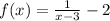
DOMAIN is set of input values for which the function is real and has defined values.

So, The given function is undefined at x = 3

So, Domain is
`x<3\quad \mathrm{or}\quad \:x>3`

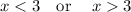
RANGE is the set of values of dependent variable for which the function is defined.

Inverse of given function is
`y=(3x+7)/(x+2)`

Now, domain of inverse function is
`f\left(x\right)<-2\quad \mathrm{or}\quad \:f\left(x\right)>-2`

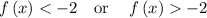
Now, x intercept and y- intercepts

x intercept where y = 0 and y- intercept where x= 0

Let f(x) = y

Then
`y=(1)/(x-3)-2`

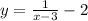
Put x = 0

thus y- intercept is
`\left(0,\:-(7)/(3)\right)`

Now put y = 0

Then x- intercept is
`\left((7)/(2),\:0\right)`

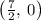
Now, Calculate the vertical and horizontal asymptotes,

Vertical asymptotes,

Go over every undefined point and check if at least one of the following statements is satisfied.

`\lim _(x\to a^-)f\left(x\right)=\pm \infty`

`\lim _(x\to a^+)f\left(x\right)=\pm \infty`

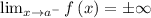
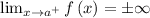
Thus, The vertical asymptotes is x = 3

And For horizontal asymptotes,

`\mathrm{Check\:if\:at\:}x\to \pm \infty \mathrm{\:the\:function\:}y=(1)/(x-3)-2\mathrm{\:behaves\:as\:a\:line,\:}y=mx+b`

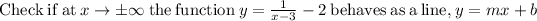
We have y = -2 as horizontal asymptotes.

Plot we get the graph as shown below.