To answer this we apply the Pythagorean Theorem, this states that given a right triangle with a hypotenuse -longest side- (

) and two sides (
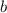
and

), then:
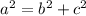
So, for your problem, we can see right triangle with a hypotenuse of 8 (
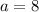
), one side equal to 4 (
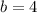
) and other side unknown; this means we have the following:
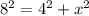
We can easily solve for

(altitude of the equilateral triangle):
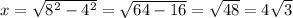 Hence, the answer is E.
Hence, the answer is E.