Question

Can someone simplify


`\frac{12 {a}^(2) {b}^(6) {c}^(5) }{20 {a}^(2) {b}^(8) {c}^(2) }`

Answer 1

`\frac{12 {a}^(2) {b}^(6) {c}^(5) }{20 {a}^(2) {b}^(8) {c}^(2) }`

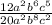
To begin, we can simplify the coefficients of the numerator and denominator:


`\frac{12 {a}^(2) {b}^(6) {c}^(5) }{20 {a}^(2) {b}^(8) {c}^(2) } = \\ \\ \frac{3 {a}^(2) {b}^(6) {c}^(5) }{5 {a}^(2) {b}^(8) {c}^(2) }`

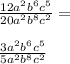
Next, the a² in both the numerator and denominator will cancel:


`\frac{3 {a}^(2) {b}^(6) {c}^(5) }{5 {a}^(2) {b}^(8) {c}^(2) } = \\ \\ \frac{3 {b}^(6) {c}^(5) }{5 {b}^(8) {c}^(2) }`

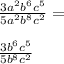
After that, we can simplify the b and c in the numerator and denominator. Keep in mind that dividing numbers with exponents (that have the same base) is the same as subtraction. For example,
`\frac{{b}^(6) }{ {b}^(8)} }= b^(6-8) = b^(-2)= (1)/(b^2)`.


`\frac{3 {b}^(6) {c}^(5) }{5 {b}^(8) {c}^(2) } = \\ \\ \frac{3 {c}^(5) }{5 {b}^(2) {c}^(2) } = \\ \\ \frac{3 {c}^(3) }{5 {b}^(2) }`


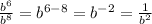
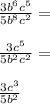
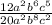
`\frac{12 {a}^(2) {b}^(6) {c}^(5) }{20 {a}^(2) {b}^(8) {c}^(2) }` simplifies to
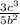
`\frac{3 {c}^(3) }{5 {b}^(2) }`.