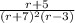So we want to divide
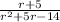
by
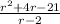
.
The first thing we are going to do is factor the denominator of the first fraction and the denominator of the second one:
- For our first fraction:
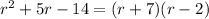
Now we can rewrite our first fraction:
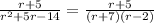
- For our second fraction:
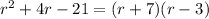
Now we can rewrite our second fraction:
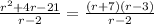
Last but not least, we can express our division as a fraction and simplify:
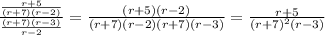 We can conclude that the result of dividing r+5/ r^2+5r-14 by r^2+4r-21/r-2 is:
We can conclude that the result of dividing r+5/ r^2+5r-14 by r^2+4r-21/r-2 is: