Question

Pyramid ABCDE is a square pyramid.

What is the lateral area of pyramid ABCDE ?

Answer 1

The lateral area of the pyramid is given by:
A = (4) * (1/2) * (b) * (h)
Where,
b: base of the triangle
h: triangle height
Substituting values we have:
A = (4) * (1/2) * (16) * (8 * tan (60))
A = 443 in ^ 2
Answer:
the lateral area of pyramid ABCDE is:
A = 443 in ^ 2

Answer 2

The lateral area of pyramid ABCDE is
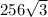`256√(3)` in².

Explanation:

According to the properties of trigonometry,

`\tan \theta=(perpendicular)/(base)`

`\tan (60^(\circ))=(height)/(8)`

`8\tan (60^(\circ))=height`

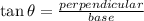
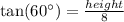
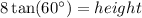
The area of a triangle is

`A=(1)/(2)* base * height`

`A=(1)/(2)* 16 * 8\tan (60^(\circ))`

`A=8* 8√(3)`

`A_1=64√(3)`

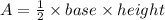
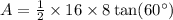
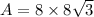
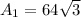
Lateral surface area of a pyramid is the sum of area of all 4 triangles. So, the lateral area of pyramid ABCDE is

`A=4* A_1`

`A=4* 64√(3)`

`A=256√(3)`

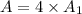
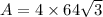
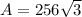
Therefore the lateral area of pyramid ABCDE is
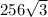`256√(3)` in².