Question

.580 80 repeating as fraction

Answer 1

To express the repeating decimal .5808... as a fraction, we can use the concept of infinite geometric series. The fraction equivalent is 580/999.

Step-by-step explanation:

The question is asking us to express the repeating decimal .5808... as a fraction. To solve this, we can use the concept of infinite geometric series. Let x represent .5808...

1. Multiply both sides of the equation by 1000 to remove the decimal: 1000x = 580.8808....
2. Subtract the original equation from the previous step: 1000x - x = 580.8808... - .5808...
3. Simplify the equation: 999x = 580
4. Divide both sides by 999 to solve for x: x = 580/999

Therefore, the decimal .5808... can be written as the fraction 580/999.

Answer 2

first off, we'll move the non-repeating part in the decimal to the left-side, by doing a division by a power of 10.

then we'll equate the value to some variable, and move the repeating part over to the left as well.

anyhow, the idea being, we can just use that variable, say "x" for the repeating bit, let's proceed,


`\bf 0.580\overline{80}\implies \boxed{\cfrac{5.80\overline{80}}{10}}\qquad \textit{now, let's say }x= 5.80\overline{80}\\\\ -------------------------------`


`\bf thus\qquad \begin{array}{llll} 100\cdot x&=&580.80\overline{80}\\ &&575+5.80\overline{80}\\ &&575+x \end{array}\qquad \implies 100x=575+x \\\\\\ 99x=575\implies x=\cfrac{575}{99}\qquad therefore\qquad \boxed{\cfrac{5.80\overline{80}}{10}}\implies \cfrac{\quad (575)/(99)\quad }{10} \\\\\\ \cfrac{\quad (575)/(99)\quad }{(10)/(1)}\implies \cfrac{575}{99}\cdot \cfrac{1}{10}\implies \cfrac{575}{990}\implies \stackrel{simplified}{\cfrac{115}{198}}`

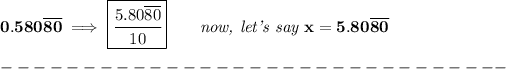
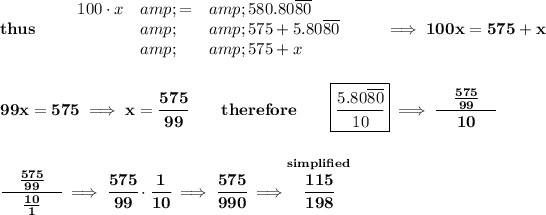
and you can check that in your calculator.