Question

What are the exact solutions of x2 − 3x − 7 = 0? x = the quantity of 3 plus or minus the square root of 37 all over 2 x = the quantity of negative 3 plus or minus the square root of 37 all over 2 x = the quantity of 3 plus or minus the square root of 19 all over 2 x = the quantity of negative 3 plus or minus the square root of 19 all over 2

Answer 1

The exact solution is:

x = the quantity of 3 plus or minus the square root of 37 all over 2

Explanation:

We are asked to find the exact solution of the polynomial equation which is given by:

`x^2-3x-7=0`

We know that the solution of the equation are the possible value of x which is obtained on solving the equation and hence satisfy the equation.

Now, on solving the quadratic equation i.e. degree 2 polynomial equation using the quadratic formula:

That is any polynomial equation of the type:

`ax^2+bx+c=0`

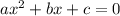
is solved by using the formula:

`x=(-b\pm √(b^2-4ac))/(2a)`

Here we have:

a=1, b=-3 and c=-7.

Hence, the solution of the equation is:

`x=(-(-3)\pm √((-3)^2-4* (-7)* 1))/(2* 1)\\\\\\x=(3\pm √(9+28))/(2)\\\\\\x=(3\pm √(37))/(2)`

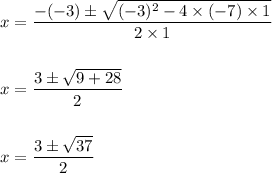
Hence, the solution is:

x = the quantity of 3 plus or minus the square root of 37 all over 2

( i.e.

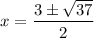`x=(3\pm √(37))/(2)` )

Answer 2

(a) x = the quantity of 3 plus or minus the square root of 37 all over 2

`x=(3\pm√(37))/(2)`

Explanation:

The given equation is a second-degree (quadratic) equation. Its solutions can be found using the "quadratic formula" applicable to such equations.

Quadratic formula

A quadratic equation written in standard form is ...

`ax^2+bx+c=0`

Its solutions are given by the formula ...

`x=(-b\pm√(b^2-4ac))/(2a)`

Application

Comparing the given quadratic to the standard form, we see the coefficients are ...

a = 1, b = -3, c = -7

Using these values in the quadratic formula gives the solutions as ...

`x=(-(-3)\pm√((-3)^2-4(1)(-7)))/(2(1))=(3\pm√(9+28))/(2)\\\\\boxed{x=(3\pm√(37))/(2)}`

The verbal description of this expression matches the first choice.