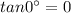Answer:
Explanation:
We have to find the values of the given trigonometric ratios at the angle indicated. Thus,
(A) The given trigonometric function is:
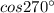
Since, the function lies in Quadrant III, therefore the value of the function will be negative.
Also,

(B) The given trigonometric function is:
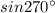
Since, the function lies in Quadrant III, therefore the value of the function will be negative.
Also,
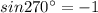
(C) The given trigonometric function is:
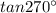
Since, the function lies in Quadrant III, therefore the value of the function will be negative.
Also,
![tan270^(\circ)=undefined]()
(D) The given function is:
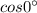
Since, the function lies in Quadrant I, therefore the value of the function will be positive.
Also,
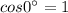
(E) The given function is:

Since, the function lies in Quadrant I, therefore the value of the function will be positive.
Also,

(F) The given function is:
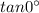
Since, the function lies in Quadrant I, therefore the value of the function will be positive.
Also,