Answer:
True
Explanation:
Given is a function of logrithm to base 0.5
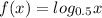
This we can write as
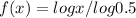
by changing the base to e.
f(x) will be decreasing if f'(x)<0
Let us find f'(x)
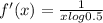
is the derivative
We know log x is defined only for positive values of x.
Hence x>0
log 0.5 is always less than 0 since 0.5<1
So f'(x) <0 for all x in the domain
This implies f(x) is decreasing
True