Question

A ball of clay with a mass of 55 g and a speed of 1.5 m/s collides with a 55 g ball of clay that is at rest. By what percent has the kinetic energy decreased after the inelastic collision?

Answer 1

The kinetic energy decreased 50 % after the inelastic collision.

Step-by-step explanation:

Since both ball collide and experiments an inelastic collision, the final velocity of the system is found by means of the Principle of Linear Momentum:

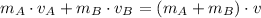`m_(A)\cdot v_(A) + m_(B)\cdot v_(B) = (m_(A)+m_(B))\cdot v` (1)

Where:

`m_(A)`,
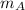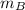`m_(B)` - Masses of the balls of clay, measured in kilograms.

`v_(A)`,
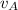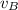`v_(B)` - Speeds of the balls of clay before collision, measured in meters per second.

`v` - Speed of the system after collision, measured in meters per second.

If we know that
`m_(A) = m_(B) = 0.055\,kg`,
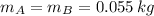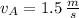`v_(A) = 1.5\,(m)/(s)` and
`v_(B) = 0\, (m)/(s)`, then the speed of the system after collision is:

`v = (m_(A)\cdot v_(A)+m_(B)\cdot v_(B))/(m_(A)+m_(B))`

`v = ((0.055\,kg)\cdot \left(1.5\,(m)/(s) \right)+(0.055\,kg)\cdot \left(0\,(m)/(s) \right))/(0.110\,kg)`

`v = 0.75\,(m)/(s)`

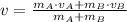
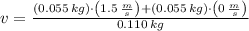
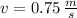
The initial (
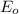`E_(o)`) and final kinetic energies of the system (
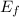`E_(f)`), measured in joules, are now described by the following equations:

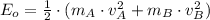`E_(o) = (1)/(2)\cdot (m_(A)\cdot v_(A)^(2)+m_(B)\cdot v_(B)^(2))` (2)

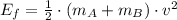`E_(f) = (1)/(2)\cdot (m_(A)+m_(B))\cdot v^(2)` (3)

And the percentage of lost energy due to inelastic collision is:

`\%e = \left(1-(E_(f))/(E_(o)) \right)* 100\,\%` (4)

If we know that
`m_(A) = m_(B) = 0.055\,kg`,
`v_(A) = 1.5\,(m)/(s)`,
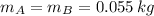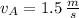`v_(B) = 0\, (m)/(s)` and
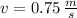`v = 0.75\,(m)/(s)`, then the percentage of lost energy due to inelastic collision is:

`E_(o) = (1)/(2)\cdot \left[(0.055\,kg)\cdot \left(1.5\,(m)/(s) \right)^(2)+(0.055\,kg)\cdot \left(0\,(m)/(s) \right)^(2)\right]`

`E_(o) = 0.062\,J`

`E_(f) = (1)/(2)\cdot (0.110\,kg)\cdot \left(0.75\,(m)/(s) \right)^(2)`

`E_(f) = 0.031\,J`

`\%e = \left(1-(0.031\,J)/(0.062\,J) \right)* 100\,\%`

`\%e = 50\,\%`

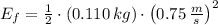
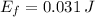
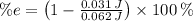
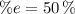
The kinetic energy decreased 50 % after the inelastic collision.