Question

The scores of eighth-grade students in a math test are normally distributed with a mean of 57.5 and a standard deviation of 6.5. From this data, we can conclude that 68% of the students received scores between and .

Answer 1

Approximately 68% of a normal distribution lies within one standard deviation of the mean, so this corresponds to students with scores between (57.5 - 6.5, 57.5 + 6.5) = (51, 64)

Answer 2

As given, the scores of eighth-grade students in a math test are normally distributed with a mean of 57.5 and a standard deviation of 6.5.

This means that around 68% of the distributed data lies within the ranges of -6.5 to +6.5 of the given standard deviation.

This implies to:

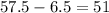`57.5-6.5=51` and
`57.5+6.5=64`

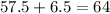
So, the range of scores lies between (51,64)