Question

Julian wants to build a rectangular pen. He plans to use a wall of his barn for one side of the pen. He has 76 yards of fencing material. What is the maximum area that can be enclosed?

Answer 1

I think it is 19 by 19 which would be 361 Yards squared.

Answer 2

Length of fencing material = 76 yards

Since, Julian is using a wall of his barn for one side of the pen, he needs fencing for three sides only.

Let the two sides be x and x. The third side opposite to barn will be = 76 - 2x

For a reactngle, we know that:

Area = length * breadth

A = x * (76 - 2x)

A = 76x -
`2x^(2)`

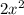
Now, to find the maximum area we need to differentiate the area with respect to x.

`(dA)/(dx) =(d)/(dx) (76x - 2x^(2))`

`(dA)/(dx) = 76 - 4x`

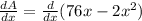
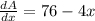
Now putting
`(dA)/(dx) = 0`

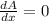
76 - 4x = 0

4x = 76

x = 76 / 4

x = 19

Other side of the pan = 76 - 2x

= 76 - 2*19

= 76 - 38

= 38

Hence, the two sides of the pan for maximum area = 19 yards and 38 yards

Therefore, the maximum area that can be enclosed = length * breadth

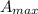`A_(max)` = 19 * 38

= 722 sq. yards