First, we are going to find the distance traveled by the ship adding the tow distances:
Distance traveled= 24 mi +33 mi=57 mi
Next, we are going to use the Pythagorean theorem to find the distance from

to

:
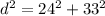
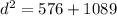
d^2=1665
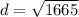
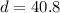
mi
Finally, we are going to subtract the two distances:
57 mi -40.8 mi= 16.2 mi
We can conclude that
if the ship could have traveled in a straight lime from point a to point c, it could have saved 16.2 miles.