Question

Evaluate the series shown. Then write an equivalent series using summation notation such that the lower index starts at 0.

∑^3 n=1 2(n+5)



FAST

Answer 1

Sample Response: Substitute the values 1, 2, and 3 into the expression 2(n + 5), then find the sum. The summation is equal to 12 + 14 + 16 = 42. You can rewrite the summation as the sum of 2(n + 6) from 0 to 2.

Answer 2

The summation indicates the sum from n = 1 to n = 3 of the expression 2(n+5).

2 (n+5) = 2n + 10

2n + 10 denotes an Arithmetic Series, with a common difference of two and first term as 12.

For n =1, it equals 12
For n = 2, it equals 14
For n = 3, it equals 16

So the sum from n=1 to n=3 will be 12 + 14 + 16 = 42

Sum of an Arithmetic Series can also be written as:


`S_(n) = (n)/(2)(2a_(1) +(n-1)d)`

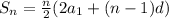
Using the value of a₁ and d, we can simplify the expression as:


`S_(n) = (n)/(2) (24+2(n-1)) \\ \\ S_(n) =n (12+(n-1))\\ \\ S_(n) =n (11+n)`

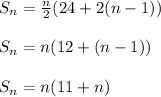
This expression is equivalent to the given expression and will yield the same result.

For n=3, we get the sum as:

S₃ = 3(11+3) = 42