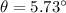Question

1.)A soccer ball is kicked with a speed of 22m/s at an angle of 35.0º above the horizontal. If the ball lands at the same level from which it was kicked, how long was it in the air?

2.)On the Apollo 14 mission to the moon, astronaut Alan Shepard hit a golf ball. The acceleration due to gravity on the moon is 1/6 of its value on the earth (gravity on moon -1.633m/s2). On earth, golf balls are driven at about 84 m/s with a loft angle of about 15º and have a range of about 353 meters. Given the same initial speed and loft angle as on the earth, what was (a) the time of flight for the golf ball and (b) what was the range on the moon?


3.)In 1975, coming out of retirement, the daredevil Evel Knievel successfully jumped over 14 Greyhound buses (a total of 40.5m). To do so, he drives his motorcycle up an incline at a speed of 44.7m/s (about 100mi/hr). What minimum angle should the ramp be in order to clear the buses?

Answer 1

1) The motion of the ball on the two axis is:

`x(t)=v_0 \cos \theta t`

`y(t)=h+v_0 \sin \theta t - (1)/(2)gt^2`
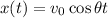
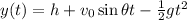
where
h is the initial height from which the ball is thrown

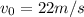
`v_0 = 22 m/s` is the initial speed of the ball

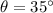
`\theta=35^(\circ)` is the angle

`g=9.81 m/s^2` is the gravitational acceleration

We want to find the time t at which the ball lands at the same altitude from which it was kicked, so the time t at which y(t)=h. Therefore:

`h+v_0 \sin \theta t - (1)/(2)gt^2 = h`
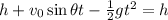
whose solutions are:

`t=0` --> this is the beginning of the motion, we are not interested in this one

`t= (2 v_0 \sin \theta)/(g)= (2 (22 m/s) (\sin 35^(\circ)))/(9.81 m/s^2)=2.57 s`
So, the ball remained in air for 2.57 s.

2) The motion of the ball on the Moon is given by:

`x(t)=v_0 \cos \theta t`

`y(t)=v_0 \sin \theta t - (1)/(2)gt^2`
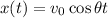
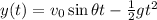
where

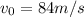
`v_0 = 84 m/s` is the initial speed of the ball

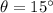
`\theta=15^(\circ)` is the angle

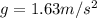
`g=1.63 m/s^2` is the gravitational acceleration on the Moon

2a) The time of flight of the ball is the time t at which the altitude of the ball returns to zero: y(t)=0, therefore

`v_0 \sin \theta t - (1)/(2)gt^2 = 0`
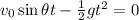
from which we find 2 solutions

`t=0` --> this is the beginning of the motion, we are not interested in this one

`t= (2 v_0 \sin \theta)/(g)= (2 (84 m/s) (\sin 15^(\circ)))/(1.63 m/s^2)=26.7s`
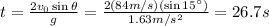
So, the time of flight of the ball on the Moon is 26.7 s.

2b) The range on the Moon is the distance covered on the x-axis during this time t=26.7 s:

`x(t)= v_0 \cos \theta t=(84 m/s)(\cos 15^(\circ))(26.7 s)=2166 m`

3) The motion of the motorcycle on the two axis is:

`x(t)=v_0 \cos \theta t`

`y(t)=v_0 \sin \theta t - (1)/(2)gt^2`
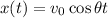
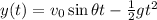
where

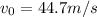
`v_0 = 44.7 m/s` is the initial speed of the motorcycle

`\theta` is the angle of the ramp

`g=9.81 m/s^2` is the gravitational acceleration
We are given the range the motorcycle covers on the x-axis, which corresponds to the length of the 14 buses: x(t)=40.5 m. At this time t, the motorcycle also comes again to the initial altitude, y=0. So we have a system of 2 equations:

`40.5 = v_0 \cos \theta t`

`0= v_0 \sin \theta t - (1)/(2)gt^2`
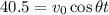
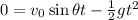
If we isolate t from the first equation:

`t= (40.5)/(v_0 \cos \theta)`
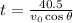
and we substitute it into the second one, we find

`0= (40.5 v_0 \sin \theta)/(v_0 \cos \theta)- (1)/(2)g ((40.5)^2)/(v_0^2 (\cos \theta)^2)`
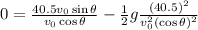
which can be rewritten as

`\sin 2 \theta = g (40.5)/(v_0^2)`
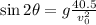
From which we find

`\theta=5.73^(\circ)`