Question

On average, Colby has noticed that 21 trains pass by his house daily (24 hours) on the nearby train tracks. What is the probability that at most 6 trains will pass his house in a 12-hour time period

Answer 1

10.16% probability that at most 6 trains will pass his house in a 12-hour time period

Explanation:

We are dealing with the mean during a period of time, so we use the Poisson distribution to solve this question.

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

Colby has noticed that 21 trains pass by his house daily (24 hours)

We are working with 12 hour periods(half of 24), so
`\mu = (21)/(2) = 10.5`

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

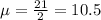
What is the probability that at most 6 trains will pass his house in a 12-hour time period

`P(X \leq 6) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6)`

So

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-10.5)*(10.5)^(0))/((0)!) = 0`

`P(X = 1) = (e^(-10.5)*(10.5)^(1))/((1)!) = 0.0003`

`P(X = 2) = (e^(-10.5)*(10.5)^(2))/((2)!) = 0.0015`

`P(X = 3) = (e^(-10.5)*(10.5)^(3))/((3)!) = 0.0053`

`P(X = 4) = (e^(-10.5)*(10.5)^(4))/((4)!) = 0.0139`

`P(X = 5) = (e^(-10.5)*(10.5)^(5))/((5)!) = 0.0293`

`P(X = 6) = (e^(-10.5)*(10.5)^(6))/((6)!) = 0.0513`

`P(X \leq 6) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) = 0 + 0.0003 + 0.0015 + 0.0053 + 0.0139 + 0.0293 + 0.0513 = 0.1016`

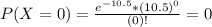
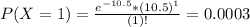
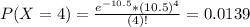
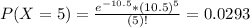
10.16% probability that at most 6 trains will pass his house in a 12-hour time period