In the given exponential decay model, we are solving for age of the painting in t years.
A represents the amount of carbon-14 at t.
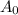
represents the original amount of carbon-14. This would be 100%.
So plug in what we know and solve for t:
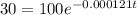
Divide both sides by 100:
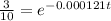
Cancel out the e by finding the natural logarithm of both sides:
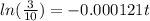
Finally, divide both sides by -0.000121:
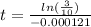
Now use a calculator to find t:
t = 9950.188
To the nearest integer, the answer is 9950 years.