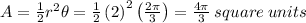Question

An equilateral triangle with side of 2 square root 3 is inscribed in a circle. What is the area of one of the sectors formed by the radii to the vertices of the triangle? 1.33 sq. in. 2 sq. in. 2.09 sq. in.

Answer 1

1.33

Explanation:

Answer 2

Refer to the figure.

We are looking for the area of the sector of a circle as shown in the figure shaded with green color.

The area of a sector of a circle can be calculated using the formula
`A=(1)/(2)r^2sin\left(\theta \right)`
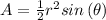
where r=radius, and θ=central angle (in radians)

The central angle of the given sector is just one-third of a full circle (2π). That is

`\theta =(2\pi )/(3)`

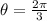
Now, to solve for the radius of the circle, we can use the formula

`R=(abc)/(4A)`
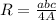
where R is the radius of the circumscribed circle; a,b, and c are the sides of the triangle; and A is the area of the triangle.

The area of the equilateral triangle can be solved using the formula
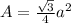
`A=(√(3))/(4)a^2`. That is

`A=(√(3))/(4)a^2=(√(3))/(4)\left(2√(3)\right)^2=3√(3)`

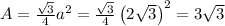
Now, we substitute this area in the formula to solve for the radius of the circle.

`R=(abc)/(4A)=(\left(2√(3)\right)^3)/(4\left(3√(3)\right))=2`

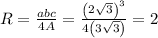
Finally, we can solve for the area of the sector by substituting the values of the angle θ, and the radius.

`A=(1)/(2)r^2\theta =(1)/(2)\left(2\right)^2\left((2\pi )/(3)\right)=(4\pi )/(3)\:square\:units`