The length of one side of the octagon is given by:
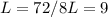
Then, the apothem can be determined using the Pythagorean theorem in the following way:
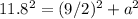
Clearing to have:
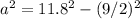
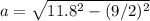
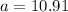
Then, the area is given by:
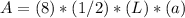
Where,
L: length of the octagon sides
a: apotema
Substituting values:
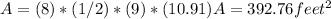 Answer:
Answer:
the approximate length of the apothem is:
a = 10.91 feet
The approximate area of the floor of the gazebo is:
A = 392.76 feet ^ 2