Question

Task Below are the heights of the players on the University of Maryland women's basketball team for the 2017-2018 season and the heights of the players on the women's field hockey team for the 2018 season.

Note: it is typical for a women's field hockey team to have more players than a women's basketball team would.


Field Hockey Player Heights (inches)

66 in. 68 in 67 in.65 in 66 in.60 in.64 in.


Field Hockey Player Heights (inches) 60 in.

64 in.69 in.64 in.68 in.66 in.66 in.


Field Hockey Player Heights (inches) 67 in 63 in.66 in.65 in 66 in.65 in.67 in.


Field Hockey Player Heights (inches) 68 in 63 in.66 in.70 in.68 in.


Basketball Player Heights (inches) 75 in 72 in.68 in.73 in.72 in.69 in.72 in.72 in.

74 in.

75 in.


1. Field Hockey Players:

Find the Measures of Center and Variability for Field Hockey Players Heights. Mean:

Mode:

Median:

Range

Answer 1

Part 1:

Arrangement of the heights of the field hockey players in a frequency distribution table is as follows:

Height: 60 63 64 65 66 67 68 69 70

Frequency: 2 2 3 3 7 3 4 1 1

The mean is given by


`\bar{x}= (\Sigma fx)/(\Sigma f) \\ \\ = (2(60)+2(63)+3(64)+3(65)+7(66)+3(67)+4(68)+69+70)/(2+2+3+3+7+3+4+1+1) \\ \\ = (120+126+192+195+462+201+272+69+70)/(26) = (1,707)/(26) \approx65.7`


Part 2:

The mode is the observation with the highest frequency.

Here, 66 has a frequency of 7 which is the highest frequency.

Therefore, the mode is 66.


Part 3:

The median is the observation in the middle after the data set has been arranged in order.

The median position is given by
`(n+1)/(2) = (26+1)/(2) = (27)/(2) =13.5`

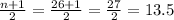
The 13.5th observation is the average of the 13th and the 14th observations.

The 13th and the 14th observations are both 66, therefore, the median is 66.


Part 4:

The range is the difference between the largest value and the smallest value.

Here, the largest value is 70 and the smallest value is 60.

Therefore, the range is given by 70 - 60 = 10.