Question

A model rocket is launched from the ground with an initial velocity of 120 feet per second. The height of an object h, in feet, after t seconds, with initial velocity v0 and initial height h0 is given by h(t)=−16t2+v0t+h0 . What is the approximate maximum height the rocket reaches?

Answer 1

567 is the height it reaches

Answer 2

The rocket will reach a maximum height of 225 feet from the ground in 3.75 seconds.

Explanation:

We are given the following information in the question:

Initial velocity =
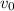`v_0` = 120 feet per second

Initial heigth =
`h_0`

`h(t) = -16t^2 + v_0t + h_0`

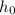
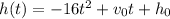
h(t) is a function of t that gives height of the rocket at time t, initial velocity
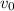`v_0`. intial height
`h_0`.

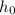Differentiating h(t) with respect to t, we get:

`\displaysttyle(d(h(t)))/(dt) = -32t + v_0`

Equating the first derivative to zero,

`-32t + v_0 = 0\\-32t = -120 \\t = \displaystyle(120)/(32) = 3.75`

Again differentiating, h(t) with respect to t,

`\displaysttyle(d^2(h(t)))/(dt^2) = -32 < 0`

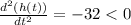
Hence, h(t) will have a local maxima by double derivative test.

Maximum height attained by rocket =

`h(\displaystyle(120)/(32)) = -16* (120)/(32)* (120)/(32) + 120* (120)/(32) + 0 = 225 \text{ feet}`

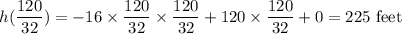
Hence, the rocket will reach a maximum height of 225 feet from the ground in 3.75 seconds.