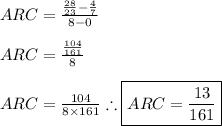
Answer:
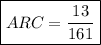
Explanation:
For a nonlinear graph whose slope changes at each point, the average rate of change between any two points
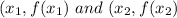 is defined as the slope of the line through the two points. We call the line through the two points the secant line and its slope is denoted as
is defined as the slope of the line through the two points. We call the line through the two points the secant line and its slope is denoted as
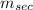 , so:
, so:
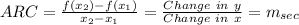
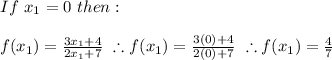
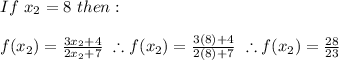
Then: