To the pair be parallel, it must meet the (Mr = Ms) rule, Slope of the R line = Slope of the S line.
*The letters used to refer the lines could be any
I will designate the first line equation as "R" and the second "S".
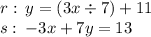
Now we have to adjust the "S" line to the Slope-Intercept form:

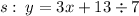
To see better which is each term, i will make another little adjust:
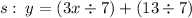
I will let the "R" line here too to view.
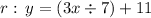
Now we have to identify which terms are the Slopes (Mr, Ms) of the equations:
y = mx + n
-> s: y = 3x/7 + 11
-> Ms = 3/7 ; Ns = 11
-> r: y = 3x/7 + 13/7
-> Mr = 3/7 ; Nr = 13/7
Now see if they meet the condition (Mr = Ms):
3/7 = 3/7
Answer: The pair is parallel because the Slope of each line has the same value.