Question

Example 2:

For this example use the function F(x)=1/2 x+1 and initial value of 4. Note that with each successive iteration you can use the previous output as your new input to the function.

4) Choose an initial value that is less than zero what happens to the value of the function as the number of iterations increases?
5) Come up with a new linear function that has a slope that falls in the range -1 6) use the function g(x) = -x +2 with the initial values of 4, 2, and 1. What happens after many iterations with all three initial values? How do the results of all three iterations relate to each other

Answer 1

Taking this example into account, we can see that setting the first value equal to 1, we obtain that
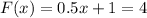
`F(x)=0.5x+1=4` and
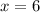
`x=6`. Using this information, we find that
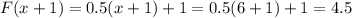
`F(x+1)=0.5(x+1)+1=0.5(6+1)+1=4.5`. It shows that when x is positive, the succussive terms are increasing.

Referring to that finding, if we set initial value less than zero, which means that we are solving 0.5x+1<0 and taking a number in the interval of the solution, which means x ∈ (- ∞, -20). Setting x=-19, we find that
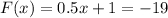
`F(x)=0.5x+1=-19` and x=-40. In the next iteration,
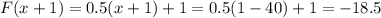
`F(x+1)=0.5(x+1)+1=0.5(1-40)+1=-18.5`. In the next iteration,
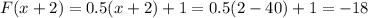
`F(x+2)=0.5(x+2)+1=0.5(2-40)+1=-18`. By this way, we find that even if the initial value is less than zero, value of the successive iterations is increasing.

Using the function
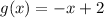
`g(x)=-x+2` and taking the initial value equal to 4, we find that
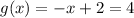
`g(x)=-x+2=4` and x=-2. In the next iteration,
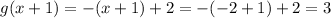
`g(x+1)=-(x+1)+2=-(-2+1)+2=3`. If we continue the iterations we'll see that they are decreasing.
Setting the initial value equal to 2, we find that
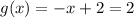
`g(x)=-x+2=2` and x=0. The next iteration is
`g(x+1)=-(x+1)+2=1`. In this case, the interations are also decreasing.
If we set the initial value equal to 1, we find that
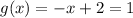
`g(x)=-x+2=1` and x=1. In the next iteration,
`g(x+1)=-(x+1)+2=0` and the iterations are decreasing.