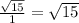Question

If cos(x)=1/4 what is sin(x) and tan(x)

Answer 1

Let us think about the trigonometric functions. If we have a right triangle with an angle we call x. Then we define the trigonometric functions as follows:

cos x = adj/hyp

sin x = opp/hyp

tan x = opp/adj

Where opp is the measure of the side opposite the angle x, adj is the measure of the side adjacent to angle x and hyp is the hypotenuse (the longest side).

We are told that cos x = 1/4 which means that the ratio of the side adjacent to the hypotenuse is 1/4. So let’s make adjacent = 1 and the hypoytenuse = 4.

We now have two sides of the right triangle but are missing the third. We use the Pythagorean theorem to find the third side. The Pythagorean Theorem says:


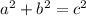
`a^(2) + b^(2) = c^(2)` where and b are the lengths of the legs of a right triangle and c is the hypotenuse. For our triangle c = 4, a = 1 and b is the side we don’t know. We could have made b = 1 and solved for a instead since a and b are both legs and can be used interchangeably.

So we end up with the following:

`1^(2)+ b^(2) = 4^(2) 1+b^(2)=16 b ^(2)=15 b= √(15)`

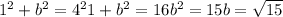
This means that the opposite side =
`√(15)`

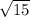
As a reminder:
opp =
`√(15)`
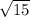
Adj = 1
hyp = 4

Therefore we find sin x and tan x as follows:

sin x = opp/hyp =
`( √(15) )/(4)`

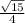
tan x = opp/adj =
`( √(15) )/(1)= √(15)`