To solve this we are going to use the exponential function:
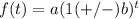
where
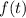
is the final amount after

years

is the initial amount

is the decay or grow rate rate in decimal form

is the time in years
Expression A
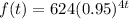
Since the base (0.95) is less than one, we have a decay rate here.
Now to find the rate

, we are going to use the formula:

*100%
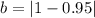
*100%
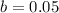
*100%
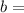
5%
We can conclude that expression A decays at a rate of 5% every three months.
Now, to find the initial value of the function, we are going to evaluate the function at

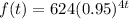
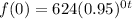
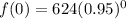
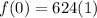
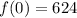
We can conclude that the initial value of expression A is 624.
Expression B
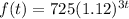
Since the base (1.12) is greater than 1, we have a growth rate here.
To find the rate, we are going to use the same equation as before:

*100%
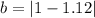
*100

*100%
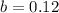
*100%
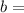
12%
We can conclude that expression B grows at a rate of 12% every 4 months.
Just like before, to find the initial value of the expression, we are going to evaluate it at

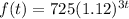
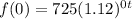

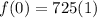
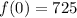
The initial value of expression B is 725.
We can conclude that you should select the statements:
- Expression A decays at a rate of 5% every three months, while expression B grows at a rate of 12% every fourth months.
- Expression A has an initial value of 624, while expression B has an initial value of 725.