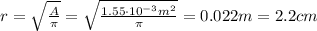Question

A solenoid with 3,000.0 turns is 70.0 cm long. If its self-inductance is 25.0 mH, what is 5) its radius? (The value of o is 4 × 10-7 N/A2.)

Answer 1

The self-inductance of a solenoid is given by:

`L= (\mu_0 N^2 A)/(l)`
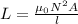
where

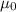
`\mu_0` is the vacuum permeability
N is the number of turns
A is the cross-sectional area of the solenoid
l is the length of the solenoid

For the solenoid in our problem, N=3000, l=70.0 cm=0.70 m and the self-inductance is L=25.0 mH=0.025 H, therefore the cross-sectional area is

`A= (Ll)/(\mu N^2)= ((0.025 H)(0.70 m))/((4\pi \cdot 10^(-7)N/A^2)(3000)^2)= 1.55 \cdot 10^(-3)m^2`
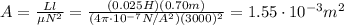
And since the area is related to the radius by

`A=\pi r^2`
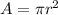
The radius of the solenoid is

`r= \sqrt{ (A)/(\pi) } = \sqrt{ (1.55 \cdot 10^(-3) m^2)/(\pi) } =0.022 m=2.2 cm`