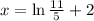Answer:
Option B is correct
Explanation:
Given the equation:
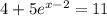 ......[1]
......[1]
Subtraction property of equality states that you subtract the same number to both sides of an equation.
Subtract 4 to both sides in equation [1];
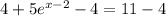
Simplify:
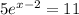
Divide both sides by 5 we get;
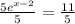
Simplify:
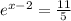
Taking log both sides we get;
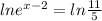
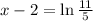 Using :
Using :
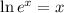
Add 2 to both sides of an equation:
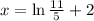
Therefore, the solution to
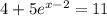 is,
is,