Question

For the set {3, 4, 5, 8,x), the

mean, median and mode all
have the same value. What
is the value of x that would
make this true?
Your lunch costs $10.95 at a

Answer 1

x = 5

Explanation:

Mode: The most frequently occurring data value.

Median: The middle value when all data values are placed in order of size.

Mean: The sum of all data values divided by the total number of data values.

As the mode is the most frequently occurring data value, x must be 3, 4, 5 or 8.

If the mode is 3 or 4, then the data set will be {3, 3, 4, 5, 8} or {3, 4, 4, 5, 8}. Therefore, the median would be 4.

If the mode is 5 or 8, then the data set will be {3, 4, 5, 5, 8} or {3, 4, 5, 8, 8}. Therefore, the median would be 5.

Therefore, the median is 4 or 5.

`\boxed{\sf mean=\frac{\textsf{sum of all the numbers}}{\textsf{amount of numbers}}}`

If x = 4, the mean would be:

`\sf \implies mean=(3+4+5+8+4)/(5)=(24)/(5)=4.8`

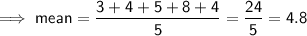
If x = 5, the mean would be:

`\sf \implies =(3+4+5+8+5)/(5)=(25)/(5)=5`

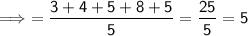
Therefore, the only value of x that allows the mean, median and mode to all have the same value is x = 5.