Question

Tan x=-1. please explain

Answer 1

If
`-\frac\pi2<x<\frac\pi2` (which is the domain of
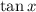
`\tan x`), then
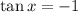
`\tan x=-1` for
`x=\tan^(-1)(-1)=-\tan^(-1)1=-\frac\pi4`.
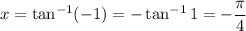
But also, recall that
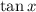
`\tan x` has period
`\pi`, which means
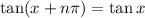
`\tan(x+n\pi)=\tan x` for all integers
`n`. This means the general solution to
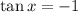
`\tan x=-1` is
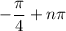
`-\frac\pi4+n\pi` for
`n\in\mathbb Z`.

This doesn't match any of the given choices, but we can simply write


`x=-\frac\pi4+n\pi=-\frac\pi4+\pi+(n-1)\pi=\frac{3\pi}4+(n-1)\pi`

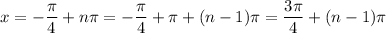
and we can just replace
`n-1` with
`n`, since both can be arbitrary integers, which means (D) is the correct answer.