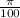Question

A baseball is hit inside a baseball diamond with a length and width of 90 feet each. What is the probability that the ball will bounce on the pitchers mound, if the diameter of the mound is 18 feet? Assume that the ball is equally likely to bounce anywhere in the infield. When applicable, leave your answer in terms of pie and include all necessary calculations.

Answer 1

90(squared) + 90 (squared) = C (squared)
(we use 90 because the base path is 90 ft long since the diamond is a square that makes all sides 90 ft long)
8100 + 8100 = c(squared)
16200 = c(squared)
we will get the square root of 16200 to get the diagonal length
C=127.3 ft, and since it is the diagonal distance we will device it to 2, to get the distance from the pitcher ro the 2nd base.
127.3/2 = 67.7 ft.
67.7 ft is the distance from the pitcher to the 2nd base.

Answer 2

`(\pi )/(100)`

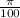
Explanation:

The first thing to notice is that the diamond is just a square rotated 45 degrees square, with 90 feet sides, so the total area of the diamond is:

A(square)= l x l = 90 ft * 90 ft = 8100
`ft^(2)`

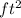
We also need to calculate the area of the mound, assuming it being a circle:

A(circle)=
`\pi * r^(2)` And r=diameter/2= 18 ft/2 = 9 ft

A(circle) =
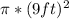`\pi * (9 ft)^(2)` = 81
`\pi ft^(2)`

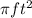
Now since the ball has an equal chance of bouncing anywhere in the field, the probability would be the ratio of the area occupied by the mound inside of the diamond.

P=
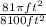`(81\pi ft^(2))/(8100 ft^(2))`=
`(\pi )/(100)`