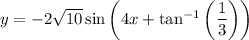Question

I don't understand number 5

Answer 1

If you expand the desired form, you get


`a\sin(bx+c)=a(\sin bx\cos c+\cos bx\sin c)`

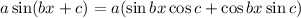
and if we match this up with the given form, we can see that
`b=4`, and we have to find
`a` and
`c` such that


`\begin{cases}a\cos c=-6\\a\sin c=-2\end{cases}`

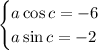
If we divide the second equation by the first, we have


`(a\sin c)/(a\cos c)=(-2)/(-6)\iff\tan c=\frac13`

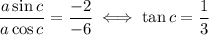
If we assume
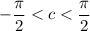
`-\frac\pi2<c<\frac\pi2`, then we can take the inverse tangent of both sides to get
`c=\tan^(-1)\left(\frac13\right)`. If we do this, then we find


`a\sin\left(\tan^(-1)\left(\frac13\right)\right)=\frac a{√(10)}=-2\implies a=-2√(10)`

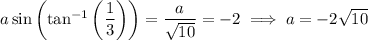
So we can rewrite


`y=-6\sin4x-2\cos4x`

as


`y=-2√(10)\sin\left(4x+\tan^(-1)\left(\frac13\right)\right)`