Question

A simple pendulum is constructed by hanging a 3 kg mass on the end of a 0.8 m long string. The pendulum is pulled back to a height of 0.2 m and released. At what time will the mass first reach its maximum velocity

Answer 1

The time when the mass will reach its first maximum velocity is 1.8 s.

Step-by-step explanation:

Given;

mass of the pendulum, m = 3 kg

length of the pendulum, l = 0.8 m

height in which the pendulum is raised to, h = 0.2 m

the mass will reach its first maximum velocity when it returns to its initial position, i.e at the middle (x = 0).

the distance between the initial position of the pendulum and the height in which it is raised is the maximum displacement (A).

If we form a right angle triangle with respect to the height in which the pendulum is raised;

the height of the right triangle, H = L - 0.2 = 0.8 - 0.2 = 0.6 m

the hypotenuse side, = L = 0.8 m

the base of the triangle (opposite side) = A

A² = L² - H²

A² = (0.8)² - (0.6)²

A² = 0.28

A = √0.28

A = 0.529 m

The maximum velocity of the pendulum is calculated as;

`V_(max) = A \omega\\\\V_(max) = A \sqrt{(g)/(l) } \\\\V_(max) = (0.529)\sqrt{(9.8)/(0.8) }\\\\V_(max) = 1.852 \ m/s`

The period is calculated as;

`V_(max) = A\omega\\\\V_(max) = A ((2\pi)/(T) )\\\\T = (2\pi A )/(V_(max))\\\\T = (2\pi \ * \ 0.529)/(1.852) \\\\T = 1.8 \ s`

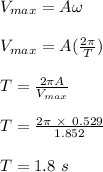
Therefore, the time when the mass will reach its first maximum velocity is 1.8 s.