Question

Write h(x) = x2 – 4x – 3 in vertex form and then identify the transformations of its graph. The function h written in vertex form is h(x) = (x – )2 + . To graph the function h, shift the graph of f = x2 right units and down units.

Answer 1

h(x) = (x – 2)2 - 7

This is because you can find the vertex to be (2, -7) using the x value of the vertex as -b/2a and the y equal to the output of that. You can then plug them into the vertex form equation.

Answer 2

Answer: Vertex form
`y=(x-2)^2-7`.

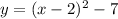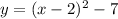`y=(x-2)^2-7` is the shifted 2 units right and 7 units down.

Step-by-step explanation: Given function f(x)=
`x^2-4x-3.`

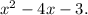
We need to write it in vertex from.

In order to write it in vertex form, we need to find the values of a, b and c for the given quadratic function.

a=1, b=-4 and x=3.

x-coordinate of the vertex = -b/2a = - (-4)/2(1) = 4/2 = 2.

Plugging x=2 in given function to get the value of y-coordinate of the vertex.

`f(2) = (2)^2-4(2)-3 = 4-8-3 =-7.`

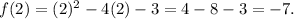
Therefore, we got vertex (h,k) at (2,-7)

Plugging values of a, h and k in vertex form
`y=a(x-h)^2+k`

`y=(x-2)^2-7`.

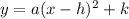
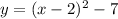Therefore, vertex form is
`y=(x-2)^2-7`.

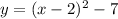Given parent function
`f(x)=x^2.`

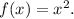
According to rules of transformations,

y=f(x-m) will translate m units right and

y= f(x) - n will translate n units down.

Therefore,
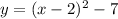`y=(x-2)^2-7` is the shifted 2 units right and 7 units down.