Question

The four vertices of a rectangle drawn on a complex plane are defined by 1 + 4i, -2 + 4i, -2 – 3i, and 1 – 3i. The area of the rectangle is square units.

Answer 1

The area of rectangle =21 sq units .

Explanation:

Given the four vertices of rectangle are 1+4i,-2+4i, -2-3i and 1-3i.

Consider ABCD is a rectangle and its vertices are 1+4i,-2+4i,-2-3i and 1-3i.

First we find sides of rectangle

AB=vertices of B- vertices of A

AB= -2+4i-(1+4i)=-3

If complex number=a+bi

Then modulus=
`√(a^2+b^2)`

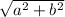
Length of AB=
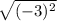`√((-3)^2)`=3 ( Because magnitude = length always positive )

BC= Vertices of C - vertices of B

BC=-2-3i-(-2+4i)=-7i

Length of BC=
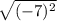`√((-7)^2)`=7 ( Magnitude always positive)

CD= vertices of D- vertices of C

CD= 1-3i-(-2-3i)=3

Length of CD=
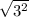`√(3^2)`=3 ( Magnitude always positive)

DA= vertices of A - vertices of D

DA= 1+4i-(1-3i) =7i

Length of DA=
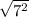`√(7^2)`=7 ( Magnitude always positive)

AB=CD and DA= BC

Length BC=7 units

Breadth AB=3 units

Area of the rectangle =
`length* breadth`

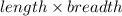
Area of rectangle =
`AB* BC`

Area of rectangle=
`3* 7`=21 sq units .

Answer 2

The rectangle is 1-(-2) = 3 units in the real direction and 4i-(-3i) = 7 units in the imaginary direction. Its area is 3×7 = 21 square units.