Question

Cube shaped boxes of tissues are shipped to stores in containers. The containers are rectangular prisms. The edges of each tissue box measure 6.5 inches The dimensions of the shipping container are 19.5 inches by 39 inches by 19.5 inches. What is the greates number of tissue boxes that will fit into one shopping container?

Answer 1

I will first calculate the volume of the tissue boxes, that are cubes.

Volume = Base Area x Height

The base area of a cube is a square so:
Base Area (Square) = L^2

In the cube, all sides have the same measure so the height is also L.

L = 6.5 in

Volume (Cube) = L^2 x L = L^3
-> Volume (Cube) = (6.5)^3
-> Volume (Cube) = approximately 275 in^3

Now calculate the Shipping Container volume:
*Represented on the photo, sorry for the bad drawing

The shipping container is a rectangle prism, every rectangle prism have on the base a square, and a square must have every sides with the same measure, knowing that, we know that the two 19.5 inches measures in the question is the length and width of the square. And the 39 inches measure is the Height of the prism.

Base Area (Square) = L^2 = (19.5)^2 = 380,25 in^2 = approx. 380 in^2
Height = 39 in

Volume = Base Area x Height
-> Volume (Prism) = 380 x 39 = 14,820 in^3

Now, to find the greatest number of tissue boxes (cubes) that fit into one container, you just need to divide the container volume by the cube volume and the quotient will be the number of tissue boxes into the container.

Cube's Volume = 275 in^3
Rectangular Prism's Volume = 14,820 in^3


`14820 / 275 = 53.8909....`
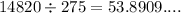
Answer: 53 tissue boxes.