Question

A truck engine slows down from 3700 rpm to 1800 rpm in 4.25 s. How many revolutions were made by the engine during this time

Answer 1

194.81 revolutions

Step-by-step explanation:

Given that,

Initial angular velocity,
`\omega_i=3700\ rpm`

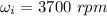
Final angular velocity,
`\omega_f=1800\ rpm`

Time, t = 4.25 seconds

We need to find the number of revolutions occur during this time.

3700 rpm = 387.46 rad/s

1800 rpm = 188.49 rad/s

Let
`\alpha` is angular acceleration. Using first equation to find it.

`\alpha =(\omega_f-\omega_i)/(t)\\\\\alpha =(188.49 -387.463 )/(4.25)\\\\\alpha =-46.81\ rad/s^2`

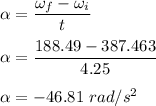
Now let us suppose that the number of revolutions are
`\theta`.

`\theta=(\omega_f^2+\omega_i^2)/(2\alpha)\\\\=(188.49 ^2-387.463 ^2)/(2* -46.81)\\\\=1224.087\ rad`

or

`\theta=(1224.087)/(2\pi)\\\\=194.81\ rev`

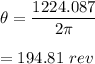
Hence, there are 194.81 revolutions.