Question

A grocery store manager received two shipments of oranges. According to the distributor of the oranges, the oranges in both shipments were equivalent because all of the oranges ranged in weight from 140 to 190 grams. The grocery store manager decided to weigh a sample of 25 oranges from each shipment to compare the weights of the oranges. The line plots show the manager's results

Based on these samples, which statement is true about the two shipments of oranges?


The two shipments have about the same mean weight but a different range of weights.

The two shipments have a different mean weight and a different range of weights.

The two shipments have about the same mean weight and the same range of weights.

The two shipments have the same range of weights but a different mean weight.

Answer 1

The answer is
The two shipments have the same range of weights but a different mean weight.
Hope i helped

Answer 2

We have been given two line plots which represents the data weight of 25 oranges of two shipments created by grocery store manager.

We have to find which of the given statements are true. To answer our problem we have to find the range and mean of the given data.

The range of a data set can be calculated subtracting the lowest value of data set from highest value of data set. By subtracting lowest value from highest value of both of our data set we get

`190-140=50`

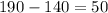
Since both data sets have same highest and lowest values our range is same that is equal to 50.

Now we will find mean of both data sets. Let us start with shipment 1 data.

Mean of shipment 1 =
`(140+145+150+2(155)+2(160)+3(165)+4(170)+5(175)+3(180)+2(185)+190)/(25)\\ =(4215)/(25)\\ =(843)/(5)=168.6`

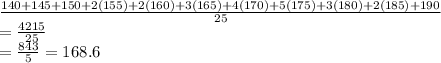
Now we will find mean of shipment 2.

Mean of shipment 2 =
`(140+3(145)+5(150)+4(155)+3(160)+2(165)+2(170)+2(175)+180+185+190)/(25) =(4000)/(25) =160`

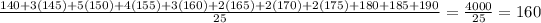
After calculating mean of both data sets we get mean of both data sets are different. Now look at the provided options which is equivalent to our answer.

The last option is correct because we got the same result in our answer that two shipments have the same range of weights but a different mean weight.