Question

Sweatshirts were on sale at the local gift shop. The cost to produce the shirts was C=0.4n^2- 32n + 650 where C is cost in dollars and n is number of shirts produced. How many shirts were produced to minimize the cost? What was the minimum cost?

Answer 1

The cost to produce n shirts is given as:


`C=0.4 n^(2) -32n+650`

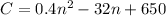
The cost function is a quadratic function with a positive leading coefficient, so the minimum value will be at the vertex of the function.

The vertex of a quadratic function can be calculated as:


`( (-b)/(2a),f( (-b)/(2a)))`

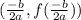
a = coefficient of squared term = 0.4
b = coefficient of n term = -32

Using these values, we get:


`- (b)/(2a)= - (-32)/(0.8)= 40`

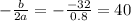This means, the cost will be minimized if 40 t shirts are produced.

The minimum cost can be found by calculating C at n=40

So, the minimum cost will be:

C(40) = 0.4(40)² - 32(40) + 650

C(40) = 10

Therefore, the minimum cost to produce a t shirt will be $10