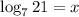Question

Which logarithmic equation is equivalent to the exponential equation below?

7^x=21

Answer 1

log base 7 (21)=x
Hope this helps!

Answer 2

`\log_721=x`

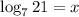
Explanation:

We have been given the exponential function
`7^x=21`

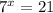
We know the relation between exponential and logarithmic function

`\text{if }y=b^x\Rightarrow\log_b(y)=x`

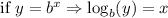
Comparing, this with the given equation, we get

y = 21

b = 7

x = x

Thus, using the relation, we have

`7^x=21\\\\=\log_721=x`

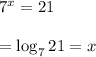
Therefore, the equivalent logarithmic equation is

`\log_721=x`