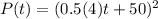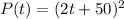Answer:
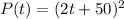
Explanation:
A certain population increases at a rate proportional to the square root of the population.
This means that the population can be described by the following differential equation:
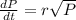
In which r is the growth rate.
Solving by separation of variables, we have that:
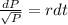
Integrating both sides:
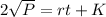
In which K is a random constant
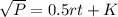
Finding the squares of both sides:
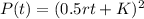
Finding the value of K
The initial population is of 2500. That is, when
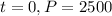 . So
. So
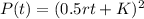
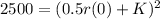
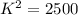
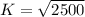
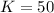
So

Finding the value of r
Population of 3600 in 5 years(when t = 5). So

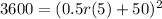
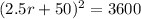
Taking the square root of both sides

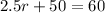
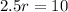

So, the equation for the population at the end of t years is given by: