Question

The force between to objects of charge +2Q and -2Q, respectively, is measured as -4F. If the charge on the first object is doubled and the distance between the objects is doubled, what will the force between the objects become?

Answer 1

-1/2F

Step-by-step explanation:

EZ WIN

Answer 2

Given two stationary charged point particles -as in your problem-, the force they feel is expressed by Coulomb's Law, written as:


`F= k(q_1q_2)/(r^2)`

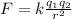
In which
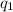
`q_1` is the charge of one of the particles,
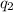
`q_2` is the charge of the other particle,
`r` is the distance between the particles, and
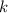
`k` is simply a constant.

From Coulomb's Law, lets assume
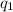
`q_1` and
`r` are doubled, what happens to
`F`?


`F=k(q_1q_2)/(r^2)`→

`k(2q_1q_2)/((2r)^2)=k(2q_1q_2)/(4r^2)= (1)/(2) k(q_1q_2)/(r^2)= (1)/(2)F`

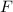
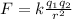
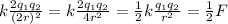So, the force is halved when you double the charge of one particle and the distance.
The answer is -2.