Question

LMN≅PQR What is the value of x in degrees? Enter your answer in the box. ​x​ = ° Coordinate graph showing triangle L M N and triangle P Q R. Triangle L M N has coordinates begin ordered pair negative 2 comma 3 end ordered pair, begin ordered pair negative 1 comma 6 end ordered pair, and begin ordered pair 1 comma 3 end ordered pair. Triangle P Q R has coordinates begin ordered pair 2 comma 1 end ordered pair, begin ordered pair 3 comma negative 4 end ordered pair, and begin ordered pair 5 comma negative 1 end ordered pair. The measure of angle L is labeled 72 degrees. The measure of angle N is labeled x degrees. The measure of angle Q is labeled 52 degrees.

Answer 1

The value of x

`x=56^(\circ)`.

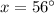Explanation:

Given

`\triangle LMN\cong \triangle PQR`

`\therefore \angle L=\angle P`

`\angle M=\angle Q`

`\angle N=\angle R`

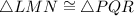
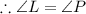
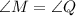
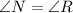
The vertices of triangle LMN at L(-2,3),M(-1,6) and N(1,3).The vertices of triangle PQR at P(2,1),Q(3,-4) and R(5,-1).

`m\angle L=72^(\circ)`

`m\angle N=x^(\circ)`

`m\angle Q=52^(\circ)`

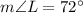
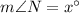
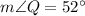
We know that
`\angle Q= \angle M=52^(\circ)`

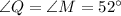
In triangle LMN

`m\angle L+m\angle M+m\angle N=180^(\circ)`

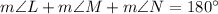
By angle sum property of angles

72+52+x=180

124+x=180

By adding property of integers

x=180-124

By subtraction property of equality

`x=56^(\circ)`

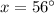
Hence, the measure of angle N=x=
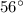`56^(\circ)`.