Question

Find an equation of the cosine function whose graph is shown below.

f(x)=____cos_____x+______

Answer 1

`y=3\text{cos}(2x)+1`

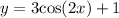
Explanation:

We have been given an image of trigonometric function. We are asked to find the equation of the given function.

We know that standard form of a cosine function is
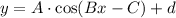`y=A\cdot \text{cos}(Bx-C)+d`, where,

A = Amplitude of function

`(2\pi)/(B)` = Period of function,

C = Horizontal shift or phase shift,

D = Vertical shift.

Upon looking at our given function we can see that amplitude of our given function is 3 as average of maximum and minimum of our given function is
`(4--2)/(2)=(4+2)/(2)=(6)/(2)=3`.

We know that mid-line of our given function is
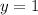`y=1`, therefore, our function is shifted upwards by 1 unit.

We can see that period of our given function is
`\pi`.

Let us find the value of B using formula:

`\pi=(2\pi)/(B)`

`B=(2\pi)/(\pi)`

`B=2`

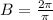
Therefore, our required equation is
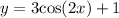`y=3\text{cos}(2x)+1`.

Answer 2

Short Answer: y = 3*cos(2x) + 1
Remark
This is not part of the answer, but it will help you to see what is going on. Begin by shifting the cos graph 1 unit down. That will that the cos has a minimum of -3 and a max of + 3

What that tells you is the part of the equation is
y = 3*cos(x)

Step One
Show that the graph is of something that resembles y = 3*cos(x)
the test way to check this is to put in 0 for x
3*cos(0) = 3*1 = 3. But why is it 4 and -2 instead of 3 and -3.

Step Two
Show how the graph is shifted up one space.
y movement is always recorded behind how the variable is determined.
So if the graph is shifting up one, you should do this.
y = 3cos(x) + 1

Step Three
The graph seems to be starting over at n*pi rather than n*2pi. How do we adjust for that?
There are 2 choices. Either there is a 4 in front of the x or there is a 1/2 in front of the x. Before just telling you, consider the graph below.
Violet is 3*cos(1/2 x)
Blue is 3*cos (x)
orange is 3*cos(2*x)

You want the graph that starts over again at x = 3.14 rather than at x = 6.28
The one that starts over at y = 3*cos(2x)
The rule is that if you want to compress a trigonometric function, use a constant such that a > 1 y = 3*cos(a*x). It is the a I'm trying to explain.

Step 4
Is there a phase shift?
No. If there was cos(x) would not have a maximum at x = 0

Answer y = 3*cos(2x) + 1