Question

A film student wants to capture a shot of a satellite dish placed at the top of a building. The line of sight between the ground camera and the top of the building is 45 feet, and the angle of the camera with respect to the ground is 50 degrees. What is the height of the building? If necessary, round your answer to the nearest tenth of a foot.

Answer 1

It is about the connection between the angles and sides of the right triangle. Let's denote the height with h. According to the sinus of the angle, we can write that sin50°=
`(h)/(45)`. It gives us
`h=45*0.76604444311=34.4719999404`. If we approximate the answer to the nearest tenth, then the final answer is 34.5 feet.

Answer 2

Please find the attachment.

Let h be the height of the building.

We have been given that the line of sight between the ground camera and the top of the building is 45 feet, and the angle of the camera with respect to the ground is 50 degrees.

We can see that line of sight between the ground camera and the top of the building will be hypotenuse of our right triangle formed by the building and the ground camera.

We can see from our attachment that h is opposite side for 50 degree angle. So we will use sine to find our side length as sine equals to opposite/hypotenuse.

`sin(50)=(h)/(45)`

`h=45\cdot sin(50)`

`h=45\cdot0.766044443119`

`h=34.471999940355\approx 34.5`

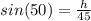
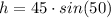
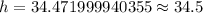
Therefore, height of the building is 34.5 feet.