Question

Please someone help fasttt

Answer 1

We'll rewrite the expression using the following properties:


`x^{ a^(b) }=x^(ab)`

`x^(a) x^(b) = x^(a+b)`

`( x^(a) )/(x^(b))= x^(a-b)`

`(a+b)^(2)=a^2+2ab+b^2`

`(a+b)(a-b)=a^2-b^2`

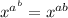
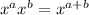
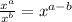
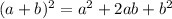
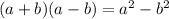
In which
`a` and
`b` are any real numbers.

So,


`(x^a)/(x^b)(a^2+ab+b^2)* (x^b)/(x^c)(b^2+bc+c^2)* (x^c)/(x^a)(a^2+ac+c^2)`

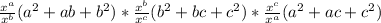
By applying the previous properties can be rewritten as:


`x^{(a-b)[ (a+b)^(2) -ab]}* x^{(b-c)[ (b+c)^(2) -bc]}* x^{(c-a)[ (a+c)^(2) -ac]}`

We keep rewriting:


`x^{(a-b)[ (a+b)^(2) -ab]+(b-c)[ (b+c)^(2) -bc]+(c-a)[ (a+c)^(2) -ac]}`

So, we need to prove the previous is equal to one.
We recall the property of exponential:


`x^(0)=1`

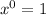
So, proving the following suffices:


`(a-b)[ (a+b)^(2) -ab]+(b-c)[ (b+c)^(2) -bc]+(c-a)[ (a+c)^(2) -ac]=0`

Proving the previous is quite simple, you can just computed directly, and you'll see that eventually everything cancels out. We can also rewrite first the expression in a more "digestible" form, as follows:


`(a-b)[ (a+b)^(2) -ab]+(b-c)[ (b+c)^(2) -bc]+(c-a)[ (a+c)^(2) -ac]=`

`(a^2-b^2)(a+b)+ab^2-a^2b+(b^2-c^2)(b+c)+bc^2-b^2c+`

`(c^2-a^2)(c+a)+a^2c-ac^2`

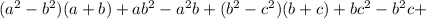
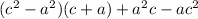
Which you can very easily shown to be equal to 0.