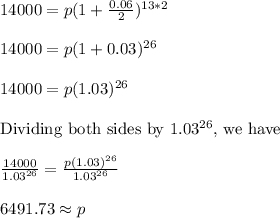Question

sonja wants to have $14000 in 13 years. calculate how much she should invest now at 6% interest, compounded semiannually in order to reach this goal

Answer 1

She should invest $6491.73.

The equation we use to solve this is in the form

`A=p(1+(r)/(n))^(nt)`,
where A is the total amount in the account, p is the principal invested, r is the interest rate as a decimal, n is the number of times per year the interest is compounded, and t is the amount of time.

A in our problem is 14000.
p is unknown.
r is 6% = 6/100 = 0.06.
n is 2, since it is compounded semiannually.
t is 13.


`14000=p(1+(0.06)/(2))^(13*2) \\ \\14000=p(1+0.03)^(26) \\ \\14000=p(1.03)^(26) \\ \\\text{Dividing both sides by }1.03^(26)\text{, we have} \\ \\(14000)/(1.03^(26))=(p(1.03)^(26))/(1.03^(26)) \\ \\6491.73\approx p`