Question

How do i find the missing sides?

Answer 1

4. You're right that the leg labeled
`x` occurs in a 1-to-2 ratio with the hypotenuse, but more to the point, it also occurs with the leg of length 10 in a 1-to-
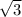
`\sqrt3` ratio. In other words,


`10=x\sqrt3\implies x=(10)/(\sqrt3)`

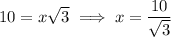
and so


`2x=(20)/(\sqrt3)`


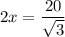
5. In this kind of triangle, the legs form a 1-to-
`\sqrt2` ratio with the hypotenuse, so it follows that
`x=2.1`.

6. You have
`x` and
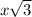
`x\sqrt3` mismatched. The larger leg in this kind of triangle has the
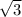
`\sqrt3` scaling factor. So in fact,
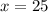
`x=25`, which makes the larger leg
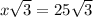
`x\sqrt3=25\sqrt3`, and the hypotenuse would be
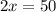
`2x=50`.