Question

What are the explicit equation and domain for a geometric sequence with a first term of 5 and a second term of −10?

an = 5(−2)n − 1; all integers where n ≥ 1
an = 5(−2)n − 1; all integers where n ≥ 0
an = 5(−15)n − 1; all integers where n ≥ 1
an = 5(−15)n − 1; all integers where n ≥ 0

Answer 1

A: an = 5(−2)n − 1; all integers where n ≥ 1

Explanation:

Answer 2

`a_(n) =5(-2)^(n-1), n\geq 1`

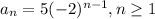
is right.

Explanation:

Given that in a geometric sequence the I term is 5 and second term is -10

If first term is a, then II term is ar where r is the common ratio

Hence r = II term/I term = -10/5 =-2

Using the geometric sequence formula for nth term

we have

`a_(n) =ar^(n-1)`

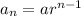
Substitute to get nth term as

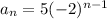`a_(n) =5(-2)^(n-1)`, for all integers n>=1

Hence option A is right answer