Question

Consider the arithmetic series:

1 + 9 + 17 + 25 + ...

Write a formula for the sum of the first n terms in this series.
A) 4n2 - 3n
B) 6n2 - 7n
C) 8n2 - 5n

Answer 1

The sum of an Arithmetic Series is given as:


`S_(n)= (n)/(2)(2a_(1)(n-1)*d)`

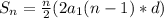
where,
d = Common Difference = Difference of any two consecutive terms.
So,
d = 8

a1 = First term = 1

Using the values, we get:


`S_(n)= (n)/(2)(2*1+(n-1)*8) \\ \\ S_(n)= (n)/(2) (2+8n-8) \\ \\ S_(n)= (n)/(2)(8n-6) \\ \\ S_(n)=n(4n-3) \\ \\ S_(n)==4n^(2)-3n`

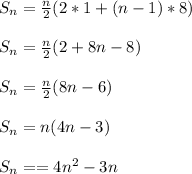
The above equation gives the formula for n terms of an Arithmetic Series.

So, option A is the correct answer